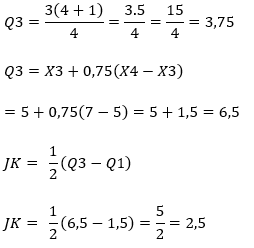Analisa Deret Berkala
Nilai semi average sebesar a0 = 502,5 merupakan nilai
trend periode desar 1 jan 97 atau 31 des 96
 à pertambahan trend
dasar tahunan secara rata-rata.
à pertambahan trend
dasar tahunan secara rata-rata.
Jadi b = (502,5 – 263,5)/4 = 59,75
Jadi persamaan kuadrat trendnya 
Jadi persamaan trend dengan tahun dasar
1993 Y’ = 263,5 + 59,75x
Jadi persamaan trend
dengan tahun dasar 1997 Y’ = 502,5 + 59,75x
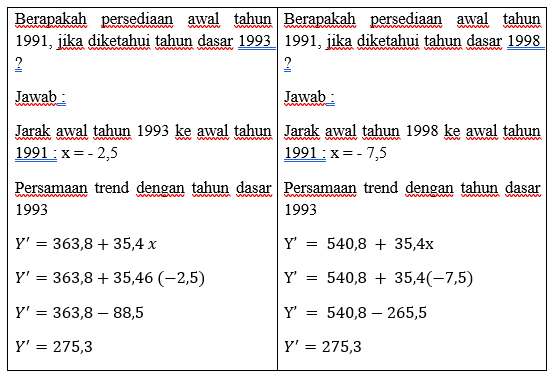
Nilai semi average sebesar a0 = 363,8 merupakan nilai
trend periode dasar Juni 1993
Nilai semi average sebesar a0 = 540,8 merupakan nilai
trend periode dasar Juni 1998
Jadi pertambahan angka diawal ada angka ½ tahun
 à pertambahan trend
dasar tahunan secara rata-rata.
à pertambahan trend
dasar tahunan secara rata-rata.
Jadi b = (540,8 – 363,8)/5 = 35.4
Jadi persamaan kuadrat trendnya 
Jadi persamaan trend dengan tahun dasar
1993 Y’ = 363,8 + 35,4x
Jadi persamaan trend dengan tahun dasar
1997 Y’ = 540,8 + 35,4x

Data diatas adalah ganjil 7 data, Jadi caranya adalah
dibagi dua – dua dulu datanya. Nanti data tengah ada 3 data dan jika di bagi
dua lagi maka ada 1 data yng 2 data dan 1 yng satu data. Maka, ditumbalkan data
tengah, jadi ada 2 data 1994. Maka ada 8 data, dan cara menghitungnya seperti
cara data genap...
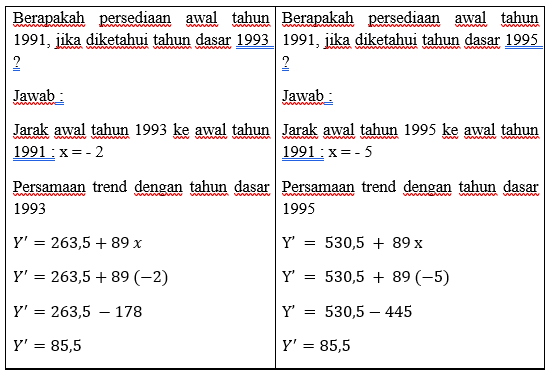
Nilai semi average sebesar a0 = 263,5 merupakan nilai
trend periode desar 1 jan 93 atau 31 des 92.
Nilai semi average sebesar a0 = 530,5 merupakan nilai
trend periode desar 1 jan 96 atau 31 des 95
 à pertambahan trend
dasar tahunan secara rata-rata.
à pertambahan trend
dasar tahunan secara rata-rata.
Jadi persamaan kuadrat trendnya 
Jadi persamaan trend dengan tahun dasar
1993 Y’ = 263,5 + 89x
Jadi persamaan trend
dengan tahun dasar 1996 Y’ = 530,5 + 89x
Data diatas adalah ganjil 7 data, Jadi caranya adalah menghilangkan
satu data tengah maka akan terbagi 2 data yang berisi data ganjil. Dan cara
mengerjakan seperti contoh no.2 dimulai dari bulan juni...
Jadi pertambahan angka diawal ada angka ½ tahun
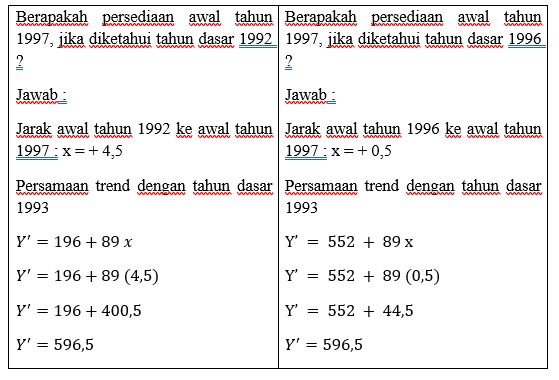
Nilai semi average sebesar a0 = 196 merupakan nilai trend
periode dasar Juni 1992
Nilai semi average sebesar a0 = 552 merupakan nilai trend
periode dasar Juni 1996
 à pertambahan trend
dasar tahunan secara rata-rata.
à pertambahan trend
dasar tahunan secara rata-rata.
Jadi persamaan kuadrat trendnya 
Jadi persamaan trend dengan tahun dasar 1992
Y’ = 196 + 89x
Jadi persamaan trend
dengan tahun dasar 1996 Y’ = 552 + 89x Regresi dan Korelasi
Regresi dan korelasi
digunakan untuk mempelajari pola dan mengukur hubungan statistika antara dua
atau lebih variabel. Jika digunakan hanya dua variabel disebut regresi dan
korelasi sederhana. Jika digunakan lebih dari dua variabel disebut regresi dan
korelasi berganda. Variabel yang akan diduga disebut variabel terikat
(tidakbebas) atau dependent variable, biasa dinyatakan dengan variabel Y. Variabel
yang menerangkan perubahan variabel terikat disebut variabel bebas atau
independent variable, biasa dinyatakan dengan variabel X. Persamaan regresi
(penduga/perkiraan/peramalan) dibentuk untuk menerangkan pola hubungan
variabel-variabel. Analisa korelasi digunakan untuk mengukur keeratan hubungan
antara variabel-variabel.
Menentukan persamaan hubungan antar variabel, langkah-langkahnya
sbb:
1.
Mengumpulkan data dari variabel yang
dibutuhkan misalnya X sebagai variabel bebas dan Y sebagai variabel tidak
bebas.
2.
Menggambarkan titik-titik pasangan (x,y)
dalam sebuah sistem koordinat bidang. Hasil dari gambar itu disebut SCATTER
DIAGRAM (Diagram Pencar/Tebaran) dimana dapat dibayangkan bentuk kurva halus
yang sesuai dengan data.
3.
Menentukan persamaan garis regresi atau
mencari nilai – nilai konstan
Analisa Regresi
Sederhana
Persamaan garis regresi
linier sederhana untuk sampel : y = a + bx, yang diperoleh dengan menggunakan Metode
Kuadrat Terkecil.
Bila diberikan data
sampel {( xi , yi ) ; i = 1,2,…,n}
Maka nilai dugaan
kuadrat terkecil bagi parameter dalam garis regresi : y = a +b x
Angka Indeks
Angka indeks adalah suatu
angka yang dibuat sedemikian rupa sehingga dapat dipergunakan untuk melakukan
perbandingan antara kegiatan yang sama (produksi ekspor, hasil penjualan,
jumlah uang beredar dsb) dalam dua waktu yang berbeda.
Didalam membuat
angka indeks diperlukan dua macam waktu yaitu :
1. Waktu
dasar yaitu waktu di mana suatu kegiatan dipergunakan untuk dasar
perbandingaan.
2. Waktu
yang bersangkutan/sedang berjalan yaitu waktu dimana suatu kegiatan akan
diperbandingkan terhadap kegiatan pada waktu dasar.
Beberapa syarat
yang perlu diperhatikan dalam menentukan atau memilih waktu dasar adalah
1. Waktu sebaiknya menunjukan keadaan
perekonomian yang stabil, di mana harga tidak berubah dengan cepat sekali.
2. Waktu sebaiknya usahakan paling lama 10
tahun atau lebih baik kurang dari 5 tahun.
3. Waktu di mana terjadi peristiwa penting.
4. Waktu di mana tersedia data untuk
keperluan pertimbangan, hal ini tergantung pada tersedianya biaya untuk
penelitian (pengumpulan data)
Kemiringan dan Keruncingan
Kemiringan distribusi data (skewness) dan keruncingan merupakan derajat atau ukuran dari ketidak simetrisan suatu distribusi data. kemiringan distribusi dibagi menjadi 3, yaitu :
1. simeteris : menujukan letak nilai rata-rata hitung, median, dan modus berhimpit
2. miring ke kanan : mempunyai nilai modus paling kecil dan rata-data hitung paling besar
3. miring ke kiri : mempunyai nilai modus paling besar dan rata-rata hitung paling kecil
1. simeteris : menujukan letak nilai rata-rata hitung, median, dan modus berhimpit
2. miring ke kanan : mempunyai nilai modus paling kecil dan rata-data hitung paling besar
3. miring ke kiri : mempunyai nilai modus paling besar dan rata-rata hitung paling kecil
Keruncingan Distribusi data merupakan derajat atau ukuran tinggi rendahnya puncak suatu distribusi data terhadap distribusi normalnya data. keruncingan distribusi data ini disebut juga kurtosis, ada tiga jenis derajat keruncingan
1. Leptokurtis adalah distribusi data yang puncaknya relatif tinggi
2. Mesokurtis adalah distribusi data yang punecaknya normal
3. platikurtis adalah distribusi data yang puncaknya rendah dan mendatar
Variansi
Apakah kalian tahu apa itu Variansi ?
Ukuran variansi dispersi merupakan ukuran penyebaran suatu kelompok data terhadap pusat data.
Macam-macam Penyimpangan :
1. Jangkauan (Range)
2. Simpangan Rata-Rata (Mean Devication)
Simpangan rata-rata merupakan jumlah nilai mutlak dari selisih semua nilai dengan nilai rata-rata dibagi banyaknya data
3. Variansi (Variance)
merupakan rata-rata kuadrat selisih atu kuadrat simpangan dari semua nilai data terhadap rata-rata hitung
4. Simpangan Baku (Standard Deviation)
merupakan akar pangkat dua dari variansi
5. Jangkauan Kuartil
disebut juga simpangan kuartil atau rentangan semi anta kuartil atau deviasi kuartil
6. Jangkauan Persentil
disebut juga simpangan persentil atau rentang semi antar kuartil deviasi persentil
Rumus dan Contoh Kasus Soal
1. Jangkauan (Range)
Data tidak berkelompok / data sebaran
A. 20, 15, 30, 70, 50 => 70 - 15 = 55
B. 50, 50, 50, 50, 50 => 50 - 50 = 0
C. 30, 40, 35, 40, 35 => 40 - 30 = 10
Dilihat dari data diatas maka, dapat dilihat jangkauan terjauhnya adalah data A
Data Berkelompok
2. Simpangan Rata-Rata (Mean Devication)
3. Variansi (Variance)
4. Simpangan Baku (Standard Deviation)
5. Jangkauan Kuartil
6. Jangkauan Persentil
Ukuran variansi dispersi merupakan ukuran penyebaran suatu kelompok data terhadap pusat data.
Macam-macam Penyimpangan :
1. Jangkauan (Range)
2. Simpangan Rata-Rata (Mean Devication)
Simpangan rata-rata merupakan jumlah nilai mutlak dari selisih semua nilai dengan nilai rata-rata dibagi banyaknya data
3. Variansi (Variance)
merupakan rata-rata kuadrat selisih atu kuadrat simpangan dari semua nilai data terhadap rata-rata hitung
4. Simpangan Baku (Standard Deviation)
merupakan akar pangkat dua dari variansi
5. Jangkauan Kuartil
disebut juga simpangan kuartil atau rentangan semi anta kuartil atau deviasi kuartil
6. Jangkauan Persentil
disebut juga simpangan persentil atau rentang semi antar kuartil deviasi persentil
Rumus dan Contoh Kasus Soal
1. Jangkauan (Range)
Data tidak berkelompok / data sebaran
A. 20, 15, 30, 70, 50 => 70 - 15 = 55
B. 50, 50, 50, 50, 50 => 50 - 50 = 0
C. 30, 40, 35, 40, 35 => 40 - 30 = 10
Dilihat dari data diatas maka, dapat dilihat jangkauan terjauhnya adalah data A
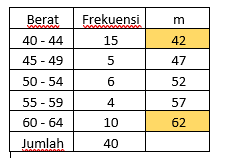
Data Berkelompok
Jangkauan Range => 62 - 42 = 20
-Semoga Bermanfaat-